Batch 3 - Class 215 - Siteswap Juggling

• Choose a starting number. Square the number and then add 1. Sum up the digits. Repeat the process till you figure out what is going on. Can you find all the loops? Can you predict which loop the number will land up in?

• Start with 3 ball juggling - show the pattern, and introduce the terminology 3-3-3. Also draw a juggling diagram to illustrate what is going on.

• Show the siteswap video to illustrate to kids what other combinations may look like and how you represent those  https://www.youtube.com/watch?v=ELvedTUcjPo
• Number of balls required in a siteswap
• How to take a siteswap and create another one from it

• Lets start back with an example - explain what this means

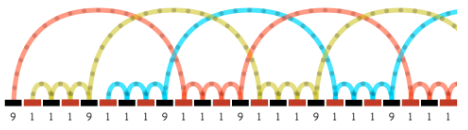
• How would you check if a particular pattern is a valid pattern. Say 6 1 2
• Write the pattern down in succession
• Choose the first ball, and trace its path through the pattern
• Do the same with other balls (how many balls do we need for this pattern?)
• You want to check that you are not throwing or catching two balls at the same time, even though good jugglers can do that

• Whats the relationship between 6 1 2 and 1 2 6 pattern?
• Whats the relationship between 6 1 2 and 6 2 1 pattern?
• None. Check and draw the second pattern
• The path that each ball follows is called an orbit. So you can break each pattern into an orbit
• For eample, for the 6 1 2 pattern, there is a 6 orbit, a 12 orbit and another 6 orbit. We can think of these as 6 0 0 orbit, and a 1 2 0 orbit to understand the number of balls in each orbit. 
• What are the number of balls in 5 6 1 pattern, and what are the orbits?
• How about 7 2 3 1 2 pattern?
• What kind of patterns do you think are valid patterns? Or what kind of patterns are not valid patterns?
• For example, 7 1 2 3 4 5 6 (draw this)

• Or, can you outline patterns that don't work. Some conjectures:
• Any positive integer repeating is a siteswap (example 3 3 3)
• Any (odd, odd) pair is a siteswap (example 3 5)
• Any (odd, even) pair fails (example 3 4)
• Any pattern having consecutive n and n-1 will fail (example ? ? ? 8 7 ? )
• If the average is an integer then the pattern is a siteswap pattern (is that true? Find counterexmple. Is the converse true?)
• Any staircase pattern is a siteswap pattern (example 1 2 3 4 5 6 7 - is that true? find counterexample)
• How about transitioning from one pattern to another one. Suppose you are throwing a 3 3 3. And now you suddenly through a 4. What can you do next? Can you transition to another pattern (such as 3 3 3 4 4 1 4 4 1 and so on)
• Interesting video demonstrating siteswap patterns  https://www.youtube.com/watch?v=B0mKbIZw7Uo

• Try and practice up to a 3 3 3 juggling siteswap!